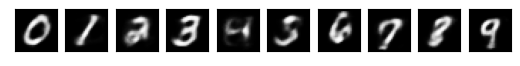Auto Encoder ✅

import torch
import torch.nn as nn
from torch.utils.data import DataLoader
import numpy as np

1 Revisiting the MNIST dataset

import torchvision
from torchvision import transforms
import my

mnist = torchvision.datasets.mnist.MNIST(
    my.DATASET_PATH,
    transform = transforms.Compose([
        transforms.ToTensor(),
    ])
)

#
# Find an example of each digit 0 .. 9
#

dataloader = DataLoader(mnist, batch_size=100)
xs, targets = next(iter(dataloader))
digits = []
for d in range(10):
    i = np.where(targets == d)[0][0]
    digits.append(xs[i])

#
# Visualize them
#
import matplotlib.pyplot as pl

for (i, x) in enumerate(digits):
    pl.subplot(1, 10, i+1)
    pl.imshow(x.squeeze(), cmap='gray')
    pl.xticks([])
    pl.yticks([])

2 Low dimensional representation with encoder

Each digit is encoded as a 28x28=784 image. This is a huge dimensionality for 10 classes.
Can we encode each digit using a much smaller vector, say 2 dimensions?
This is the function of an encoder.

\[ \mathbf{Encoder} : \mathbb{R}^{28\times 28} \to \mathbb{R}^2 \]

We can implement this using any kind of architecture – for example a simple MLP will do.

def make_encoder(DIM):
    return nn.Sequential(
        nn.Flatten(),
        nn.Linear(28 * 28, 100),
        nn.ReLU(),
        nn.Linear(100, DIM),
        nn.Tanh(),
    )

Questions?

What is the evaluation of the quality of the encoding in \(\mathbb{R}^2\)? What is the loss function?

Answers

The quality is that each encoding has enough to help a decoder to recover the input.

NOTE:

We do not make use of the labels at all in this approach.

3 Reconstruction from low dimensional representation with decoder

A decoder is a function that tries to recover the initial input from its low dimensional encoding. Namely,

\[ \mathbf{Decoder} : \mathbb{R}^2 \to\mathbb{R}^{28\times 28} \]

def make_decoder(DIM):
    return nn.Sequential(
        nn.Linear(DIM, 100),
        nn.ReLU(),
        nn.Linear(100, 28*28),
        nn.Sigmoid(),
        nn.Unflatten(1, (1, 28, 28)),
    )

4 Visualizing encoder-decoder action

def show_enc_dec(encoder, decoder, digits):
    encoder = encoder.to('cpu')
    decoder = decoder.to('cpu')
    with torch.no_grad():
        for i, x in enumerate(digits):
            x2 = decoder(encoder(x[None, :, :, :]))
            pl.subplot(1, 10, i+1)
            pl.imshow(x2.squeeze(), cmap='gray')
            pl.xticks([])
            pl.yticks([])

encoder = make_encoder(100)
decoder = make_decoder(100)

show_enc_dec(encoder, decoder, digits)

5 Training of encoder-decoder stack

The encoder-decoder stack is to recover the image.

\[ \mathbf{Decoder} \circ \mathbf{Encoder} : \mathbb{R}^{28\times 28} \to\mathbb{R}^{28\times 28} \]

We can use the original images as training data for the encoder-decoder stack.

\[ \mathbf{Training} = \{(x, x): x\in\mathbf{Dataste}\} \]

The loss function is just to compare the recovered image with the original image using mean-square error: \(\mathbf{MSE}(\mathbf{decoder}(\mathbf{encoder}(x)), x)\)

def train(encoder, decoder, dataloader, epochs, lr=0.01):
    params = list(encoder.parameters()) + \
             list(decoder.parameters())
    optimizer = torch.optim.Adam(params)
    loss = nn.MSELoss()

    encoder = encoder.to(device)
    decoder = decoder.to(device)
    
    for epoch in range(epochs):
        for x, _ in dataloader:
            x = x.to(device)
            x_out = decoder(encoder(x))
            l = loss(x_out, x)
            l.backward()
            optimizer.step()
            optimizer.zero_grad()
        print(epoch, l.item())

encoder = make_encoder(100)
decoder = make_decoder(100)

train(encoder, decoder, dataloader, epochs=1)

0 0.04748028889298439

show_enc_dec(encoder, decoder, digits)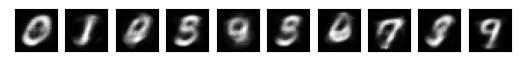

train(encoder, decoder, dataloader, epochs=1)
show_enc_dec(encoder, decoder, digits)

0 0.03105493076145649

train(encoder, decoder, dataloader, epochs=1)
show_enc_dec(encoder, decoder, digits)

0 0.023360546678304672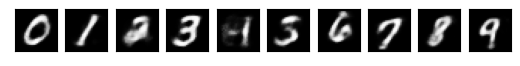

train(encoder, decoder, dataloader, epochs=1)
show_enc_dec(encoder, decoder, digits)

0 0.018861427903175354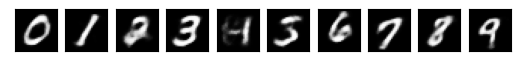

train(encoder, decoder, dataloader, epochs=1)
show_enc_dec(encoder, decoder, digits)

0 0.01599368266761303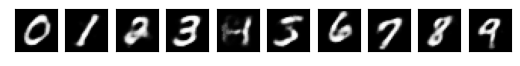

train(encoder, decoder, dataloader, epochs=1)
show_enc_dec(encoder, decoder, digits)

0 0.014078974723815918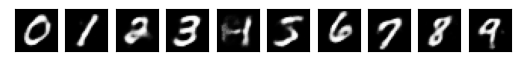

6 Going super low dimensional

e3 = make_encoder(3)
d3 = make_decoder(3)
train(e3, d3, dataloader, epochs=5)

0 0.06385622918605804
1 0.06373556703329086
2 0.0636959820985794
3 0.06369175761938095
4 0.06371547281742096

show_enc_dec(e3, d3, digits)

e10 = make_encoder(50)
d10 = make_decoder(50)
train(e10, d10, dataloader, epochs=5)

0 0.06367220729589462
1 0.0583176463842392
2 0.04323694854974747
3 0.034544687718153
4 0.02812880463898182

show_enc_dec(e10, d10, digits)