✓ Core Functional Programming¶
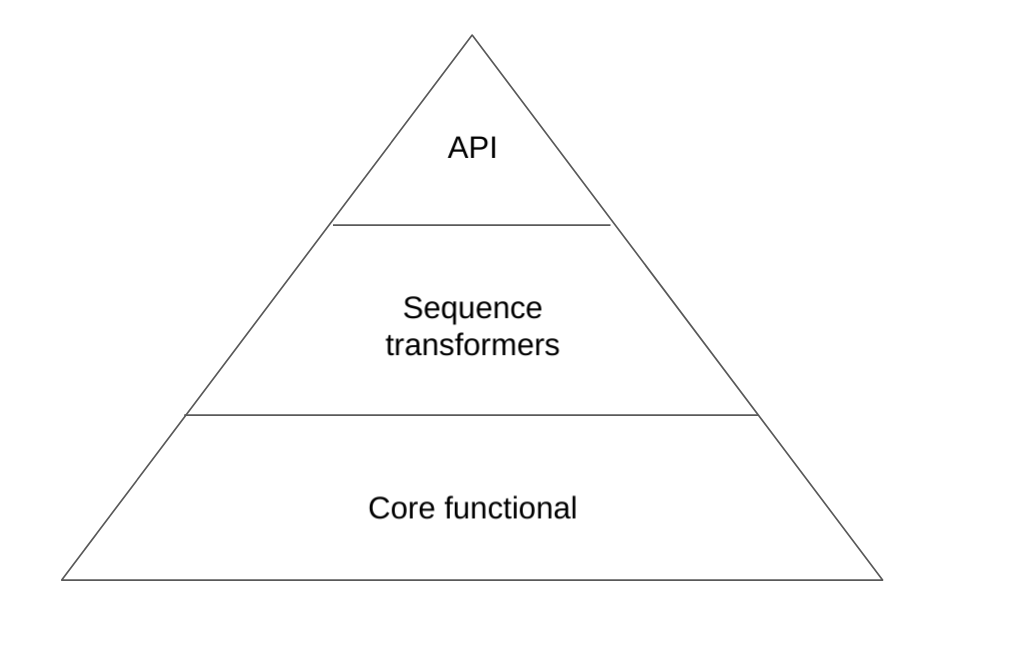
Core functional:
Branching and conditional
Sequences
Iterations
Looping
Sequence transformation
Map
Reduce
API
Domain-specific functions and data structures
Expressions¶
(do …) form¶
The do-form allows us to evaluate multiple expressions in sequence, but only the last expression will be used as the value of the do-form.
(do (+ 1 2)
"Hello"
(str "The last " "expression."))
"The last expression."
(let …) form¶
Did you know that the let-form also allows multiple expressions as part of its body. Just like the do-form, the last expression is used as the value of the let-form.
(let [x 1
y 2
z 3]
(str "x=" x)
(str "y=" y)
(str "z=" z))
"z=3"
Threading forms¶
Function composition reviews¶
(defn square [x] (* x x))
(defn to-string [x] (str "x = " x))
#'user/to-string
;;
;; A deep nested function invocation
;;
(let [x 42]
(to-string (+ (inc (- (square x) 1000)) 2.4)))
"x = 767.4"
The -> thread¶
(-> x
(f1 y1 y2 y3 ...)
(f2 z1 z2 z3 ...))
becomes
x ---+
|
|
(f1 ___ y1 y2 y3 ...) ----+
|
+--------------------+
|
|
(f2 ___ z1 z2 z3 ...)
;;
;; A different view of function composition as a pipeline
;;
(let [x 42]
(-> x
square
(- 1000)
(inc)
(+ 2.4)
(to-string)))
"x = 767.4"
The ->> thread¶
(->> x
(f1 y1 y2 y3 ...)
(f2 z1 z2 z3 ...))
becomes
x ---------------+
|
|
(f1 y1 y2 y3 ... ___) ----+
|
+--------+
|
|
(f2 z1 z2 z3 ... ___)
(to-string (+ 2.4 (inc (- 1000 (square 42)))))
"x = -760.6"
(->> 42
(square)
(- 1000)
(inc)
(+ 2.4)
(to-string))
"x = -760.6"
as-> threading¶
(to-string (+ 2.4 (inc (- (square 42) 1000))))
"x = 767.4"
(as-> 42 x
(square x)
(- x 1000)
(inc x)
(+ 2.4 x)
(to-string x))
"x = 767.4"
Branching¶
If-else¶
True:
trueor anything that is notnil.False:
falseornil.
(if (> 2 3)
"2 > 3"
"not 2 > 3")
"not 2 > 3"
(if (< 2 3)
"2 < 3"
"not 2 < 3")
"2 < 3"
(defn age-binary-category [age]
(if (< age 65)
"Not senior"
"Senior"))
#'user/age-binary-category
(age-binary-category 42)
"Not senior"
If-else is not that great¶
(defn age-many-category [age]
(if (< age 4)
"toddler"
(if (< age 12)
"preteen"
(if (< age 21)
"teen"
(if (< age 50)
"adult"
(if (< age 65)
"midlife"
"senior"))))))
#'user/age-many-category
(age-many-category 23)
"adult"
(age-many-category 13)
"teen"
(age-many-category 63)
"midlife"
Cond form¶
(defn age-category [age]
(cond
(< age 4) "toddler"
(< age 12) "pretten"
(< age 21) "teen"
(< age 50) "adult"
(< age 65) "midlife"
:else "senior"))
#'user/age-category
(age-category 23)
"adult"
(age-category 13)
"teen"
Iterations¶
Sequences: a first look¶
Lisp is all about processing lists. Clojure enriches lists with many variations which collectively are referred to as sequences.
Eager sequences are sequences whose elements are created when the sequence is created.
Lazy sequences are sequences whose elements are created only when they are needed.
Creating sequences¶
(range 10)
(0 1 2 3 4 5 6 7 8 9)
(range 10 20)
(10 11 12 13 14 15 16 17 18 19)
(range 10 20 3)
(10 13 16 19)
Range sequences are lazy.
Iteration with for-form¶
(for [i (range 5)]
(str "Iteration i:" i))
("Iteration i:0" "Iteration i:1" "Iteration i:2" "Iteration i:3" "Iteration i:4")
Using for-form as data¶
(println (clojure.string/join "\n"
(for [i (range 5)]
(str "i=" i))))
i=0
i=1
i=2
i=3
i=4
nil
(as-> 5 $
(range $)
(for [i $] (str "i=" i))
(clojure.string/join "\n" $)
(println $))
i=0
i=1
i=2
i=3
i=4
nil
for-loop with :let and :when clauses¶
(for [i (range 10)
:let [square (* i i)]
:when (even? i)]
(str "square of " i " is " square))
("square of 0 is 0" "square of 2 is 4" "square of 4 is 16" "square of 6 is 36" "square of 8 is 64")
(for ...) form with multiple bindings¶
How many pairs (x, y) of integers are there between 0 to 100 such that:
16x + y/4 is between (50, 60)
x and y are less than 10 apart
(defn is-solution? [x y] (<= 50 (+ (* 16 x) (/ y 4)) 60))
(defn close? [x y] (<= 0 (Math/abs (- x y)) 9))
#'user/close?
(let [solutions (for [x (range 100)
y (range 100)
:when (and (is-solution? x y)
(close? x y))]
[x y])]
(println "Solutions:" solutions)
(println "Count:" (count solutions)))
Solutions: ([3 8] [3 9] [3 10] [3 11] [3 12])
Count: 5
nil
Iteration without results¶
(doseq [x (range 100)
y (range 100)
:when (and (is-solution? x y)
(close? x y))]
(println "(x, y) = " x y))
(x, y) = 3 8
(x, y) = 3 9
(x, y) = 3 10
(x, y) = 3 11
(x, y) = 3 12
nil
Another variation of iteration without results¶
(dotimes [i 4]
(println i))
0
1
2
3
nil
The most general iteration¶
Loop and recur¶
(loop [ <initial-bindings> ]
<body>)
where the body must contain a recursion call of the form
(recur <new values...>)
(loop [count-down 5]
(if (pos? count-down)
(do (println count-down "...")
(recur (dec count-down)))
(println "Boom")))
5 ...
4 ...
3 ...
2 ...
1 ...
Boom
nil
(defn count-sequence [collection]
(loop [size 0
x collection]
(if (empty? x)
size
(recur (inc size) (rest x)))))
#'user/count-sequence
(count-sequence [:a :b :c])
3
(count-sequence "hello world")
11
A Case Study¶
Identify a prime number¶
(defn prime? [n]
(empty? (for [m (range 2 (dec n))
:when (zero? (mod n m))] m)))
#'user/prime?
(prime? 10)
false
(prime? 11)
true
List prime numbers by an upper limit¶
(defn prime-numbers [limit]
(for [n (range 2 limit)
:when (prime? n)]
n))
#'user/prime-numbers
(prime-numbers 100)
(2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97)
List prime numbers by count¶
(defn all-prime-numbers []
(for [n (range)
:when (and (<= 2 n) (prime? n))]
n))
#'user/all-prime-numbers
First approach: use sequence transformation
(defn get-prime-numbers [first-n]
(take first-n (all-prime-numbers)))
#'user/get-prime-numbers
(get-prime-numbers 10)
(2 3 5 7 11 13 17 19 23 29)
Second approach: use the core loop/recur
(defn loop-prime-numbers [first-n]
(loop [result []
more-numbers (all-prime-numbers)]
(cond
(= first-n (count result)) result
:else (let [n (first more-numbers)]
(recur (conj result n)
(rest more-numbers))))))
#'user/loop-prime-numbers
(loop-prime-numbers 10)
[2 3 5 7 11 13 17 19 23 29]
